|
|
atlas | summaries & slides | oa | support | dvd | contact | about | links | fb | tw | ud | nsdl | Aa | Aa |
|---|
This page contains original teaching materials and media curated from the web to accompany a pair of tutorial articles in the journal Interface Focus. The articles are available as part of a special issue on Game Theory and Cancer. The open-access costs for these articles have been generously provided by the Princeton Physical Sciences-Oncology Center, so both tutorials are available under a CC-BY 3.0 license. Skip to the bottom of this page for supplementary materials for these articles.
This is a 3 hour 30 minute tutorial workshop for beginners interested in evolutionary game theory (EGT) models. Small teams (2-3 students) can use this page as a self-guided tour. If you would like to schedule a live guided tour (online or in person), please contact David Liao (priority for NCI Physical Sciences-Oncology Network investigators and patient advocates). Simulations are Java applets that run directly off this website. You need not install MatLab.
Benefits: After using this workshop, biological scientists should be comfortable reading literature about simple evolutionary game theory models (literature samples included here). Students will likely also be comfortable performing some basic modeling on their own (i.e. studying how changing matrix elements describing pairwise interactions changes population dynamics).
Limitations: It is important to be aware that this is neither a comprehensive review of findings nor a comprehensive review of methods from evolutionary game theory research. As with the rest of this website, this workshop is in α (alpha). There are multiple ways to seek out in-depth assistance or to have modeling done for you. You could look through the conversations at the evolutionary game theory google community. You could also try to contact authors listed in the references on this page.
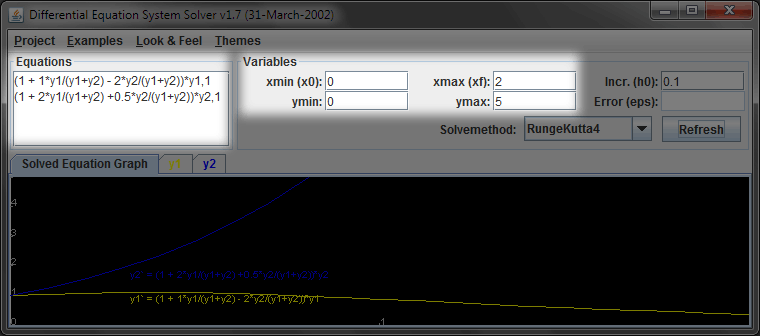
Open Jens Langer's differential equation solver by clicking the "Start DESSolver Applet" button to the right. For more information about the applet, see Dr. Langer's applet information page. Dr. Langer has released the applet under the GNU GPL license.
The example screen capture highlights two regions of the applet. Enter the following pair of expressions into the "Equations" box. If you are running into problems copying-and-pasting equations into the Java applet, this blog post by Kyle Hatlestad (Oracle) might be useful.
(1 + 1*y1/(y1+y2) -2*y2/(y1+y2))*y1,1 (1 + 2*y1/(y1+y2) +0.5*y2/(y1+y2))*y2,1The first line specifies dy1/dt, and the second line specifies dy2/dt. The ",1" appended to each line is an initial condition. Set the range of time, x, from 0 to 2 and the range of the dependent variable, y, from 0 to 5.
Read this multiple-choice prompt with a partner: Evolutionary game theory is an example of a modeling framework used in the NCI Physical Sciences-Oncology Network to understand social aspects of biological systems. What statement about evolutionary game theory is best?
This video describes a population dynamics model in which cell-cell collisions affect replication rates
Watch a video (13 minutes) | Back to topThis video describes tabular game theory and similarities with the population dynamics model in the previous video
Work with a partner to address the multiple-choice prompt from the beginning of this section.
We draw a more concrete connection between evolutionary game theory population dynamics and business transaction payoff matrix analysis. In this video, population dynamics equations are derived in a way so that it seems as though cells repeatedly face the consequences of games each time they participate in cell-cell collisions.
In the videos so far, we can identify two propositions.
How can the quantitative analyses we have explored help us to relate these propositions?
Watch a video (11 minutes) | Back to topIn this video, we provide an example how the concept of time can connect proposition 1 to proposition 2.
Glance at literature | Back to topPlease flip through figures from these papers.
We have so far focused on well-mixed models. What happens when populations are not-as-well-mixed or not mixed at all? To address this question, work through the next section following the break.
| “ |
. . . Volterra's equations for the dynamics of a predator and prey species . . . [in] a sense . . . are manifestly false. . . . . Their merit is to show that even the simplest possible model of such an interaction leads to sustained oscillation -- a conclusion it would have been hard to reach by pure verbal reasoning. --John Maynard Smith (1982) Evolution and the Theory of Games, Cambridge University Press, p. 9 |
One of the basic lessons in spatially-resolved models is that social interactions can generate different outcomes depending on whether dispersal is localized or global.
Work with a partner to address the multiple-choice prompt form the beginning of this section.
Glance at literature: We used the prisoner's dilemma in the preceding video because it is compact and simple. To see that the utility of the familiarity we have developed extends beyond this particular game, consider the game of rock-paper-scissors. In rock-paper-scissors, there are three, rather than two cell types. Additionally, there is no obvious hierarchy (unlike the prisoner's dilemma, in which defectors tend to outperform cooperators when mixed). Nonetheless, keeping mixture local (rather than global) also promotes coexistence in this system, as experimentally and theoretically explored in Kerr B, Riley MA, Feldman MW, and Bohannan JM (2002) Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature 418:171--174. Please see figures 2 and 3. The manuscript is made available at the first author's research webpage.
To play with a rock-paper-scissors style cellular automata simulation, click on the "Start MJCell" button to the right. A Java applet will launch in a separate window (example screen capture below). This applet is Mirek's Java Cellebration. Mirek Wójtowicz has made the source code available for modification. See also the list of cellular automata Java applets assembled by David Griffeath (Mathematics, University of Wisconsin).
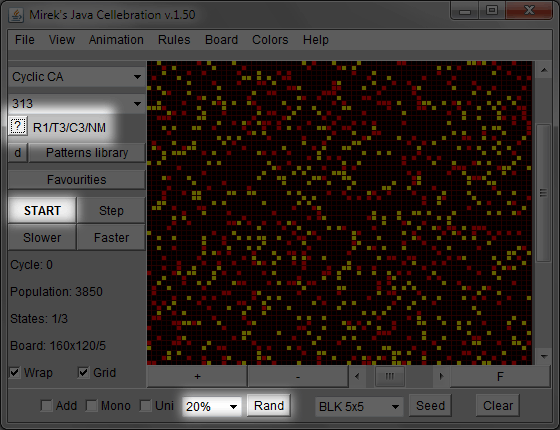
Three elements are highlighted in the example screen capture of the applet. The applet will load rule 313 from the Cyclic CA family. This is represented near the question-mark button (?) using the notation R1/T3/C3/NM.
There are three cell types (C = 3), which we can call rock, paper, or scissors. Each cell type can be replaced by a cell of the next type (rock defeats scissors, scissors defeat paper, and paper defeats rock). A cell surveys its neighbors. In this simple example, the neighbors are the 8 nearest sites (N, W, S, E, NW, SW, SE, NE) that a cell can get to by moving at most one lattice bond (horizontal, vertical, and/or diagonal). This is notated by saying the range (R = 1) is one bond (see the entry on Moore neighborhood from Wolfram MathWorld). If there are at least a threshold number of cells (here, T = 3) of "the next" cell type among the neighbors, the cell switches. For example, if rock is surrounded by 3 papers, rock becomes paper. The R/T/C/N notation is described in detail in the lexicon for the applet.
Work with a partner to address the following prompts.Are you a dork? If so, you might be interested in rock-paper-scissors-lizard-spock.
In this section, we established intuition that spatial isolation can promote heterogeneous coexistence while thorough mixture can promote homogeneity. The kind of interaction (e.g. seed dispersal and surveying of neighbors) we have discussed is, in a sense, context independent. It occurs to the same spatial extent regardless of whether the environment in which cells/plants find themselves. Life is not always so simple. An example of conditional movement occurs when parents base their decisions to leave town because they don't like the neighbors. How does conditional movement help us to refine the intuitions we have developed using the previous video? The next section provides a way to address this point.
Spend 10 minutes working through the figures on Athena Aktipis's "walk away" description. Work with a partner to practice presenting the figures in plain language.
In addition to movement, other phenotypes can be contextually triggered. For examples in ant colonies, watch the video in the next section.
In this microworkshop, we have been informal regarding the word "strategy" and "behavior." The purpose of this prompt is to encourage increased precision. Use the following prompt to start thinking about differences between "strategies" and "actions" or "behaviors." Without spending too much time on responding to the prompt, go ahead and watch the video. While Deborah Gordon's talk is not meant to address these linguistic concerns directly, the video will provide 20 minutes of distraction for your brain to "solve the problem without really directly working on the problem." After watching the video, work on the prompt for no more than about 10-15 minutes. Finally, consolidate your understanding by looking up the definition to a "complete contingency plan."
Read this prompt with a partner: Sometimes, an ant can give up a task and take on another. The fraction of time spent on a task depends on the demographic composition that the ant infers from recent ant-ant contact. How many strategies are there in each of the following situations?
Deborah Gordon (entomologist from Stanford) talks about task allocation and organization without central control in ant colonies.
Work with a partner to address the prompt at the top of this section.
The following files are from the dinner talk on Monday, 2013 August 12 given at the Princeton/Johns Hopkins Game Theory and Cancer Workshop in Baltimore, MD. This presentation has not yet been rendered into an audio-narrated video. To request to see the presentation by Skype conference, please send an email (priority for Physical Sciences Oncology Network members and patient advocates).

|
© Copyright 2011-2015 David Liao. These videos and slides are open course ware made available under a Creative Commons license (CC BY-SA 4.0). The lightbox and social sharing effects are scripts by Stéphane Caron (CC BY 2.5). |